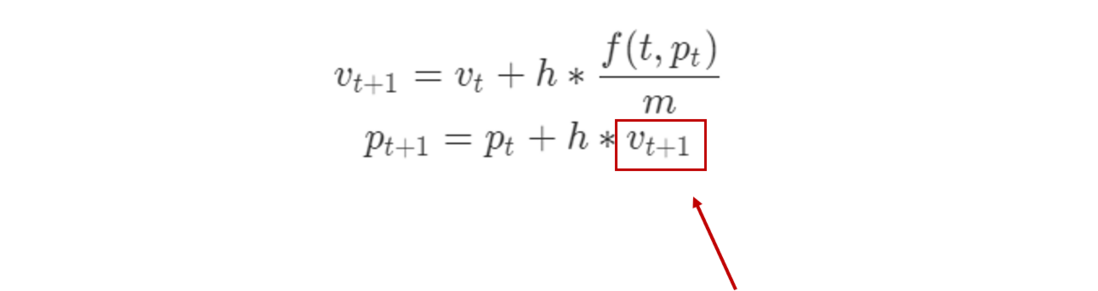欧拉的读书好方法
欧拉的读书方法介绍
欧拉是18世纪著名的数学家和物理学家,他的读书方法主要包括:勇于质疑,善于提问;注重细节,精益求精;重视逻辑思维,反复演练。欧拉的读书方法强调了对读物的深入理解和逻辑思维的训练,通过不断地提问和思考,反复推敲和演练,从而深入领会和掌握知识,培养自己的科研能力。
数学家欧拉的故事
欧拉是史上著名的,他在数论、几何学、天文数学、微积分等好几个数学的分支领域中都取得了出色的成就。不过,这个大数学家在孩提时代却一点也不讨的,他是一个被除了名的小。
事情是因为星星而引起的。 当时,小欧拉在一个教会学校里读书。有一次,他向老师,天上有多少颗星星。老师是个神学的信徒,他不天上究竟有多少颗星,上也没有回答过。其实,天上的星星数不清,是无限的。我们的肉眼可见的星星也有几千颗。这个老师不懂装懂,回答欧拉说:“天有有多少颗星星,这无关紧要,只要知道天上的星星是镶嵌上去的就够了。”欧拉感到很奇怪:“天那么大,那么高,地上没有扶梯,上帝是怎么把星星一颗一颗镶嵌到一在幕上的呢?上帝亲自把它们一颗一颗地放在天幕,他为什么了星星的数目呢?上帝会不会太粗心了呢?
他向老师提出了心中的疑问,老师又一次被问住了,涨红了脸,不知如何回答才好。老师的心中顿时升起一股怒气,这不仅是因为一个才上学的向老师问出了这样的问题,使老师下不了台,更主要的是,老师把上帝看得高于一切。小欧拉居然责怪上帝为什么没有记住星星的数目,言外之意是对万能的上帝提出了怀疑。在老师的心目中,这可是个严重的问题。
在欧拉的年代,对上帝是绝对不能怀疑的,人们只能做思想的,绝对不允许思考。小欧拉没有与教会、与上帝“保持一致”,老师就让他学校。但是,在小欧拉心中,上帝神圣的光环消失了。他想,上帝是个窝囊废,他怎么连天上的星星也记不住?他又想,上帝是个,连提出问题都成了罪。他又想,上帝也许是个编造出来的家伙,根本就不存在。
回家后无事,他就放羊,成了一个牧童。他一面放羊,一面读书。他读的书中,有不少数学书。 爸爸的羊群渐渐增多了,达到了100只。原来的羊圈有点小了,爸爸决定建造一个新的羊圈。他用尺量出了一块长方形的土地,长40米,宽15米,他一算,面积正好是600方米,均每一头羊占地6方米。正打算动工的时候,他发现他的材料只够围100米的篱笆,不够用。若要围成长40米,宽15米的羊圈,其周长将是110米(15+15+40+40=110)感到很为难,若要按原计划建造,就要再添10米长的材料;要是缩小面积,每头羊的面积就会小于6方米。 小欧拉却向父亲说,不用缩小羊圈,也不用担心每头羊的领地会小于原来的计划。他有办法。
父亲不小欧拉会有办法,听了没有理他。小欧拉急了,大声说,只有稍稍移动一下羊圈的桩子就行了。 父亲听了直摇头,心想:“世界上哪有这样便宜的事情?”但是,小欧拉却说,他一定能两全齐美。父亲终于同意让试试看。 小欧拉见父亲同意了,站起身来,跑到准备动工的羊圈旁。他以一个木桩为中心,将原来的40米边长截短,缩短到25米。父亲着急了,说:“那怎么成呢?那怎么成呢?这个羊圈太小了,太小了。”小欧拉也不回答,跑到另一条边上,将原来15米的边长延长,又增加了10米,变成了25米。经这样一改,原来计划中的羊圈变成了一个25米边长的正方形。然后,小欧拉很自信地对爸爸说:“,篱笆也够了,面积也够了。”父亲照着小欧拉设计的羊圈扎篱笆,100米长的篱笆真的够了,不多不少,全部用光。面积也足够了,而且还稍稍大了一些。父亲心里感到非常。孩子比,真会动脑筋,将来一定大有出息。
父亲感到,让这么聪明的孩子放羊实在是及可惜了。后来,他想办法让小欧拉认识了一个大数学家伯努利。通过这位数学家的推荐,1720年,小欧拉成了巴塞尔的大学生。这一年,小欧拉13岁,是这所大学最的大学生。
数学家欧拉的读书故事
欧拉出生在瑞士名城巴塞尔。他的爸爸是位神甫,酷爱数学,在爸爸的书房里,除了不多的神学书之外,满满当当的,全是数学书!从小欧拉略略懂事开始,这位热爱数学的父亲,只要有空,就会把儿子抱在大腿上,给他讲各种有趣的数学故事。
聪明的小欧拉,当然也特别喜欢听爸爸讲数学故事了。你瞧,爸爸刚下班回家,他就拽住了爸爸的黑袍子,要听故事。
“好的,”爸爸说,“今天,爸爸给你讲个关于象棋的故事。从前,印度有个国王叫舍罕。他的大臣发明了象棋。一天,刚和大臣下了一盘象棋的国王,觉得象棋非常好玩,决定重赏大臣。‘国王,’大臣说,‘您只要赏赐给我一些麦子就行了。请在棋盘的第一格里放1粒,第二格里放2粒,第三格里放4粒,第四格里放16粒……以此类推,把64格棋盘放满,就够了!’‘你只要这点赏赐啊,’国王笑得喘不过气来,立刻派人来放麦子。可是,让人想不到的是,棋盘的格子还没放到一半,国库内的麦子就搬光了。”
小欧拉睁大眼睛,出神地望着爸爸,过了好一会儿才问道:“这,怎么可能呢?”
爸爸抚摸着小欧拉的头,说:“孩子,你还不懂,这就是数学上的幂级数。如果把棋盘64格全放满麦粒的话,这些麦子得有18000亿吨。”
“18000亿吨,那是多少啊?”小欧拉闹不明白。
“哦,这样跟你说吧,假设当时印度全年小麦的生产量是100万吨的话,要生产这么多的小麦,要用一百八十万年才行。”
“我的天哪!”小欧拉惊呼起来,“原来,小小的棋盘里,竟然有如此有趣的数学问题!”
这个故事深深震撼了小欧拉的心灵,从此,一颗热爱数学的种子在小欧拉的心灵深处种下了。
一转眼,欧拉该上学了。他被送到巴塞尔文科学校学习。学校里数学课很少,这可急坏了热爱数学的欧拉。每天一回家,他就钻进爸爸的书房,找些数学书读读。一天,他取下来的是德国数学家鲁道尔夫的《代数学》。读了几页,小欧拉就被深深吸引了,他边读边思考,很快弄懂了那几页的知识,还试着做了几道练习题。
爸爸回来后,小欧拉把做的题目拿给爸爸看。“啊,你做得不错!”爸爸边看边点头。
爸爸的夸奖地激励了欧拉。他把《代数学》带到学校,一有空就自学。遇到问题时,他总是做好符号,去问老师或者爸爸。他越学越深,到后来,有些问题连大人都答不上来了。
不久,欧拉打听到当地有一位学识渊博的数学家,名叫约翰?伯克哈特。于是,在一个星期天的早晨,他敲开了伯克哈特的门。伯克哈特见小欧拉手捧《代数学》,大为吃惊,忙问:“这本书,你能读得懂?”
欧拉点点头,随即又摇摇头,说:“能懂一些,不过还有许多问题想请教您呢!”
伯克哈特不敢相信。他翻开书指着一道代数题,让欧拉来解答。欧拉看了一眼,立刻拿起笔在纸上飞快地演算着。不一会儿,答案便算出来了。
伯克哈特惊喜万分,他拉着欧拉的手,连声说:“天才!天才!”
从此,伯克哈特收下了这位还在读小学的“弟子”,他不但耐心地解答欧拉的每一个问题,而且还旁征博引地给欧拉讲述了许多代数学知识。在伯克哈特的指点下,读小学的欧拉不仅自学完了《代数学》,还学习了伯克哈特推荐的其它数学书。
在名师的指点下,通过自己的勤奋自学,13岁的欧拉,以优异的成绩,考著名的巴塞尔大学。 寒假里,我读了一篇关于欧拉的故事:
欧拉是数学史上著名的数学家,他在数论、几何学、天文数学、微积分等好几个数学的分支领域中都取得了出色的成就。不过,这个大数学家在孩提时代却一点也不讨老师的喜欢,他是一个被学校除了名的小学生。
事情是因为星星而引起的。 当时,小欧拉在一个教会学校里读书。有一次,他向老,天上有多少颗星星。老师是个神学的信徒,他不知道天上究竟有多少颗星,上也没有回答过。其实,天上的星星数不清,是无限的。我们的肉眼可见的星星也只有几千颗。这个老师不懂装懂,回答欧拉说:"天有有多少颗星星,这无关紧要,只要知道天上的星星是上帝镶嵌上去的就够了。"
欧拉感到很奇怪:"天那么大,那么高,地上没有扶梯,上帝是怎么把星星一颗一颗镶嵌到天幕上的呢?上帝亲自把它们一颗一颗地放在天幕,他为什么忘记了星星的数目呢?上帝会不会太粗心了呢?
他向老师提出了心中的疑问,老师又一次被问住了,涨红了脸,不知如何回答才好。老师的心中顿时升起一股怒气,这不仅是因为一个才上学的孩子向老师问出了这样的问题,使老师下不了台,更主要的是,老师把上帝看得高于一切。小欧拉居然责怪上帝为什么没有记住星星的数目,言外之意是对万能的上帝提出了怀疑。在老师的心目中,这可是个严重的问题。
在欧拉的年代,对上帝是绝对不能怀疑的,人们只能做思想的,绝对不允许思考。小欧拉没有与教会、与上帝"保持一致",老师就让他离开学校回家。但是,在小欧拉心中,上帝神圣的光环消失了。他想,上帝是个窝囊废,他怎么连天上的星星也记不住?他又想,上帝是个,连提出问题都成了罪。他还想,上帝也许是个别人编造出来的家伙,根本就不存在。后来,经过大数学家伯努利的推荐,1720年,小欧拉成了巴塞尔大学的大学生。这一年,小欧拉才13岁,是这所大学最年轻的大学生。
欧拉方法
比如有一段等间隔采样的加速度 a_0,a_1,...,a_n ,采样间隔为 \delta t ,在已知初始速度为 v_0 的情况下求 t_n 时刻的速度 v_n .
最简单的方法是假设两次采样间隔之间加速度不变,都是第一次采样时刻的加速度,因此有 v_n=v_0+a_0\delta t+a_1\delta t+...+a_{n-1}\delta t
也就是说给定微分方程 \dot{v}=a (注意这里自变量是时间 t ,因变量是速度 v ,加速度 a 是测量值),在已知微分方程经过点 (t_0,v_0) 的前提下,可以得到自变量任意值 t_n 对应的 v_n ,也就是得到 v 关于 t 的近似函数了(离散的)。高中牛顿力学回顾
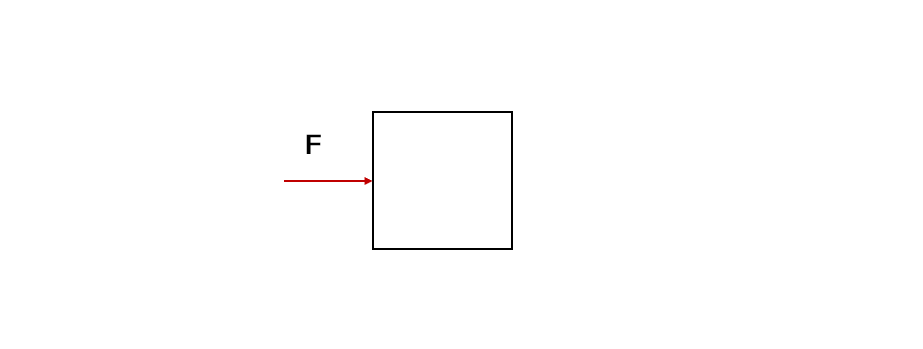
有一个具有一定速度在运动的物体:
当我们需要对其进行模拟时,自然会想起高中的 位移 = 速度 时间,即:
s=v∗ts=v∗t
而当该物体具有恒定加速度(恒力)时:
我们可以应用牛顿第二定律,求出物体在 $t$ 时间的速度:
vt=v0+Fm∗tvt=v0+Fm∗t
因此,我们想获得物体在 $t$ 时间的位置,就可以使用以下公式:
s=v0∗t+12∗Fm∗t2s=v0∗t+12∗Fm∗t2
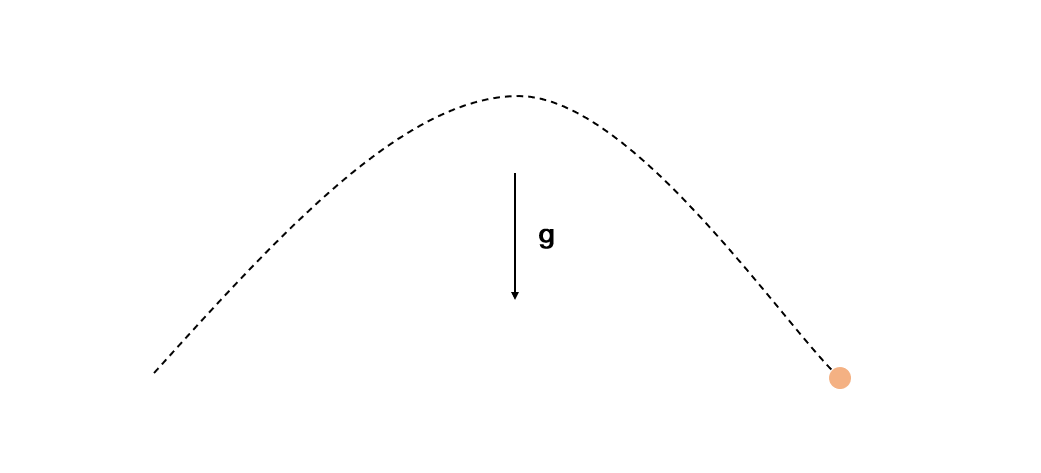
该公式在理想情况下,十分合理且正确,比如模拟一个斜方向向上抛出的小球,重力作用下(无空气摩擦),我们必定能得到一个对称的抛物线:
这都是高中物理课上我们学到的知识,对于简单的模拟已经够用了。
使用数值方法
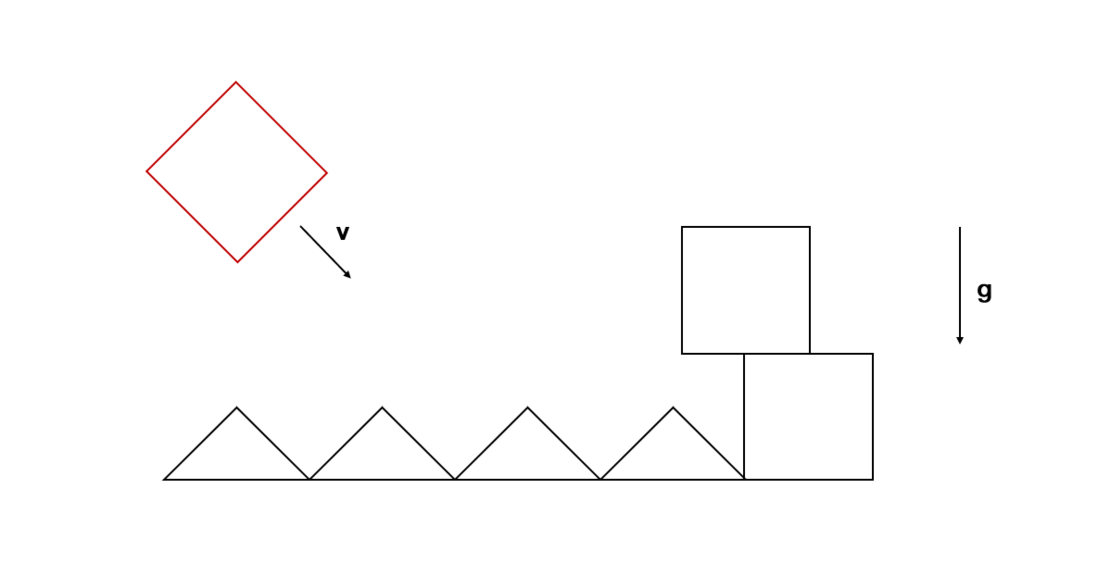
然而,我们要模拟的现实世界往往比较复杂,几乎不可能有受力恒定的情况出现,考虑以下情况:
你能写出红色盒子在之后的每一个时间 $t$ 的位置方程吗?显然这是无比困难的,因为该盒子受到的外力 $f$ 跟其位置 $p$ 有关,即 $f$ 与 $p$ 存在某种函数关系,因此,我们可以抽象出物体加速度 $a$ 与 $p$ 的关系:
a=f(t,p)ma=f(t,p)m
而又因 $a$ 为 速度 $v$ 的一阶阶导数,$v$ 为 $p$ 的一阶导数,因此我们最终得到:
p¨=v˙=f(t,p)mp¨=v˙=f(t,p)m
这是一个标准的微分方程($p$ 上面有一点表示导数),我们从该方程中直接求出 $p$ 基本上是不可能的,因 $f$ 往往很复杂(包含了各种碰撞和约束) 。但是我们可以使用数值方法。数值方法的本质上是用某种方法来近似求出我们需要的解。使用数值方法我们得不到精确解,但是没所谓,在精度要求不是十分严格的模拟下一般都够用了。
而又物体的速度 $v$ 为 $p$ 的一阶导数,我们得到:
p˙=vp˙=v
我们可以将两条微分方程组合起来,使用矩阵表示:
[v˙p˙]=[f(t,p)mv][v˙p˙]=[f(t,p)mv]
用 $\dot X$ 表示左边的矩阵,$F(t, X)$ 表示右边的矩阵,有:
X˙=F(t,X)X˙=F(t,X)
啰嗦了这么多,就是为了得到这个方程,我们的目标就是要使用数值方法求解出这个方程的 $X$。为什么要求 $X$?因为模拟的本质就是求某个物体在某一时候应该正确出现的位置(和旋转)。
求解微分方程的数值方法有许多,如 Runge Kutta,Mid-point,还有我之前介绍过的 Verlet,但我今天介绍最常用也是最基础的三种方法,分别为:
显式(向前)欧拉方法:Explicit Euler
隐式(向后)欧拉方法:Implicit Euler
半隐式欧拉方法:Semi-implicit Euler
显式(向前)欧拉方法
1. 介绍
观察我们的方程:
X˙=F(t,X)X˙=F(t,X)
求解 $X$ 不容易,但是我们可以从 $\dot X$ 入手。
回忆高中数学,若有函数 $f(x)$,那么其导数的定义为:
f˙(x)=dfdx=limh→0f(x+h)−f(x)hf˙(x)=dfdx=limh→0f(x+h)−f(x)h
但是计算机模拟是离散的,因此步长 $h$ 取不了无限小,只能是一个有一定大小的数,但是我们可以利用这种思想,对 $\dot f(x)$ 进行近似:
f˙(x)≈ f(x+h)−f(x)hf˙(x)≈ f(x+h)−f(x)h
按照这种思路我们可以求出近似的 $\dot X$。
比如,我们要求 $t_1$ 时刻的 $\dot X$,我们可以:
X˙1=F(t1,X1)=X2−X1t2−t1X˙1=F(t1,X1)=X2−X1t2−t1
其中 ${t_2 - t_1}$ 即模拟步长 $h$。那么现在我们可以求 $t_2$ 时刻的 $X$,即 $X_2$ 为:
X2=X1+h∗F(t1,X1)X2=X1+h∗F(t1,X1)
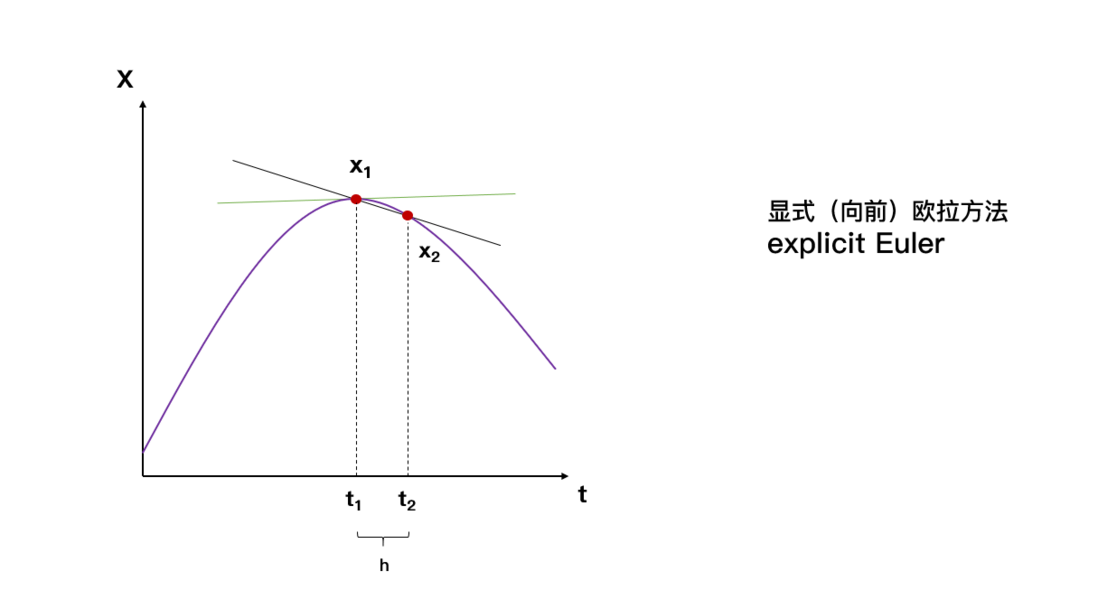
这种对于每一个时刻($t_2$),都使用上一时刻($t_1$)的解进行求解的方法即为显式欧拉方法,又叫向前欧拉方法。下图显示了显式欧拉方法的细节:
绿线为 $\dot X_{1}$ 的真实值,黑线为显式欧拉的得到的近似值,可以看到是有一定误差存在的,同时也能发现,缩短步长 $h$ 能提高精度。
显式欧拉简单高效且容易实现,但是缺点明显。
2. 稳定性分析
显式欧拉方法不是无条件稳定的方法。这句话我们要理解两个词,首先是稳定,第二是无条件。稳定指的是在长时间模拟下,得到的数值不会指数级爆炸;无条件指的是在任何微分方程下都能稳定。
因此显式欧拉方法在某些方程下能稳定,某些方程下不稳定。我们可以用以下方程来测试:
y˙(t)=−λy(t)y˙(t)=−λy(t)y(0)=y^y(0)=y^
该线性微分方程称为测试方程,其中有初始值 $\hat y$,且 $\lambda > 0$。
该方程的解为 $y = \hat y e^{-\lambda t}$,显然在 $t \to +\infty$ 时,$y \to 0$。
我们将该测试方程代入到显式欧拉方法的公式里,有:
yt+1=yt−hλyt=(1−hλ)ytyt+1=yt−hλyt=(1−hλ)yt
运用数学归纳法,我们可以得到 $y_t$ 与 $\hat y$ 的关系为:
yt=(1−hλ)tytyt=(1−hλ)tyt
显然,这是一个指数函数,因此想要在 $t \to +\infty$ 时不发生数值爆炸,我们只能限制:
$$\vert {1 - h\lambda} \vert
也就是只有当 $h\lambda > 0$ 时或 $h\lambda
隐式(向后)欧拉方法
1. 介绍
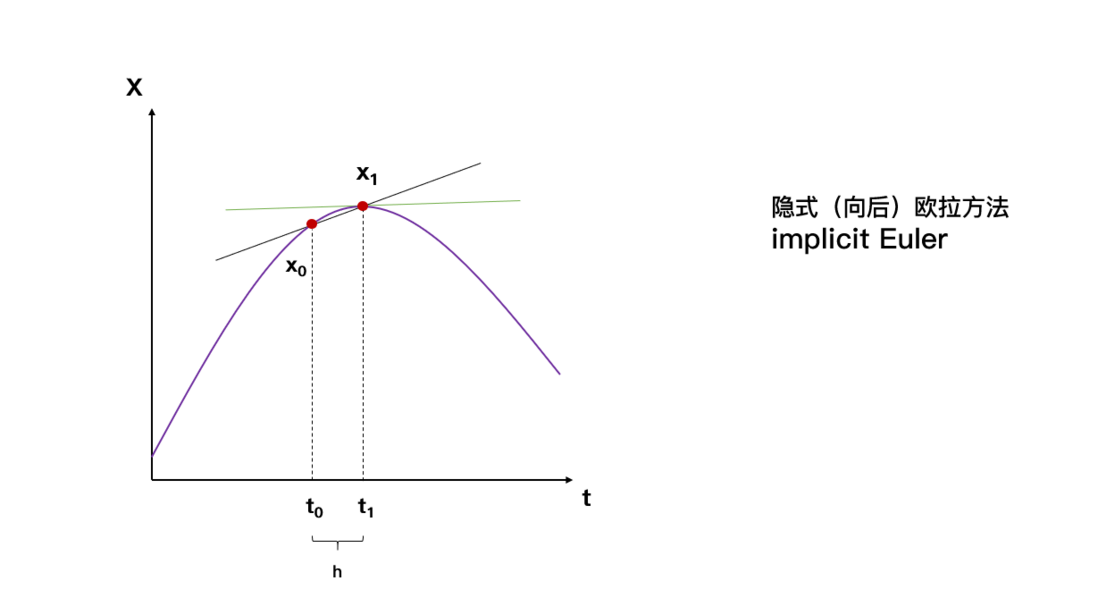
显式欧拉方法的思路是使用上一时刻的导数($F(t - 1, X_{t - 1})$)去近似当前时刻的结果($X_{t}$)。而隐式欧拉对齐进行了改进:使用当前时刻的导数($F(t, X_{t})$)近似当前时刻的结果($X_t$)。这是隐式欧拉和显式欧拉的唯一区别。用公式表示就是:
X˙1=F(t1,X1)=X1−X0t1−t0X˙1=F(t1,X1)=X1−X0t1−t0⇒X1=X0+h∗F(t1,X1)⇒X1=X0+h∗F(t1,X1)
绿线为 $\dot X_{1}$ 的真实值,黑线为隐式欧拉的得到的近似值,隐式欧拉同样也会产生误差。
也许你会发现一些问题:在 $X_1$ 未求出前,我们怎么能先计算 $F(t_1, X_1)$ 呢?没错这就是隐式欧拉方法最大的缺陷,它计算困难复杂,通常需要求解方程组,但是隐式欧拉最大的优点是数值稳定。
2. 稳定性分析
隐式欧拉方法是无条件稳定的方法。使用上面的测试方程,我们对隐式欧拉方法进行同样的操作:
yt+1=yt−hλyt+1yt+1=yt−hλyt+1
整理得:
yt+1(1+hλ)=y_tyt+1(1+hλ)=y_t
对初始值 $\hat y$ 归纳得:
yt=(11+hλ)ty^yt=(11+hλ)ty^
我们又得到了一个指数函数,同样想要不发生数值爆炸,只有:
$$\vert \frac {1}{1 + h\lambda} \vert
也就是需要 $\vert 1 + h\lambda \vert > 1$。步长 $h$ 必定是一个正数,又有 $\lambda > 0$(上面有写),因此不等式恒成立。
半隐式欧拉方法
显式欧拉和隐式欧拉都有各种的缺点,因此后人想出了一种新方法,将两者结合了起来。
现在让我们忘记 $\dot X = F(t, X)$,回到:
v˙=f(t,p)mv˙=f(t,p)mp˙=vp˙=v
对其使用显式欧拉积分,有:
vt+1=vt+h∗f(t,pt)mvt+1=vt+h∗f(t,pt)mpt+1=pt+h∗vtpt+1=pt+h∗vt
既然对两条方程都使用隐式欧拉比较难求解,那么我们就仅对较简单的那条方程使用隐式欧拉:
红框显式了该方法与显式欧拉的唯一不同之处,我们使用显式欧拉求解速度,用隐式欧拉求解位置,这种混合的方法就叫半隐式欧拉方法。
半隐式欧拉方法相比于隐式欧拉方法更容易实现,速度更快,相比显式欧拉要更稳定些,但并不是无条件稳定。在大部分情况下半隐式欧拉方法都能稳定,除了某些极端条件(比如非常大的参数)。所以半隐式欧拉在刚体模拟下是最常用,也是首推的。
总结
显式欧拉:简单,快,不稳定
隐式欧拉:复杂,慢,稳定
半隐式欧拉:简单,快,大部分情况稳定(刚体模拟首推)